Eksempler på binær til Ascii-konvertering
Inndata
ExampleUtdata
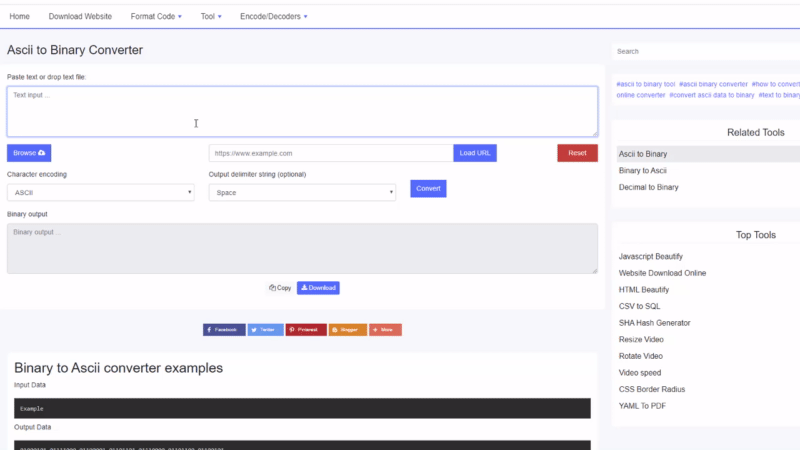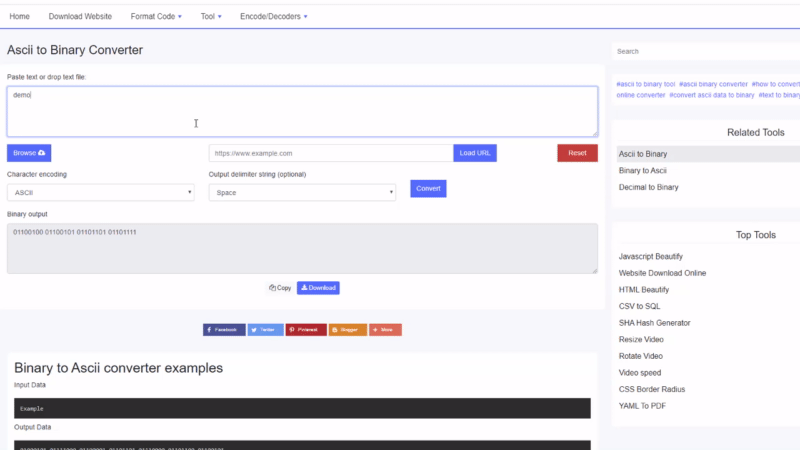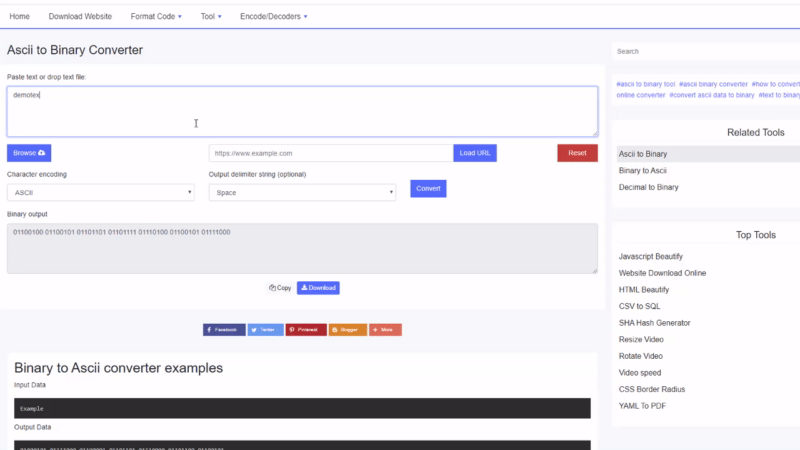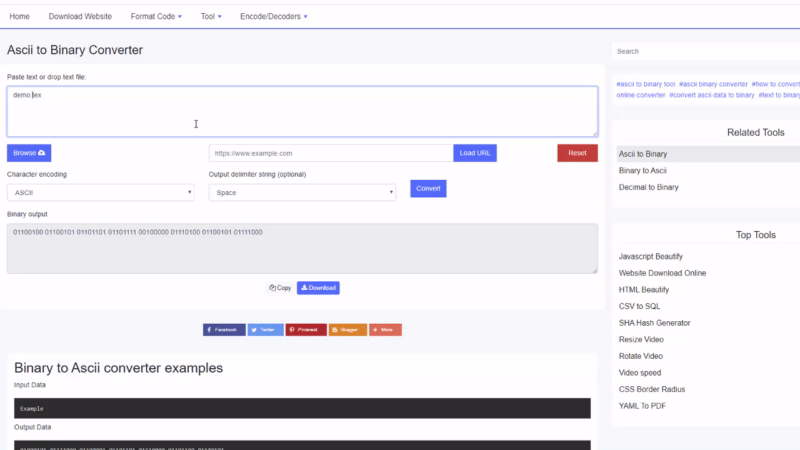
01000101 01111000 01100001 01101101 01110000 01101100 01100101Hvordan konvertere binær til tekst
Konverter tekst til binær ASCII-kode:
- Få karakter
- Få desimalkode for tegn fra ASCII-tabellen
- Konverter desimal til binær byte
- Fortsett med neste tegn
Hvordan konvertere 01000001 binær til tekst?
Bruk ASCII-tabell:
"P" => 80 = 26+24 = 010100002
"l" => 108 = 26+25+23+22 = 011011002
"a" => 97 = 26+25+20 = 011000012
'A' = 6510 = 64+1 = 26+20 = 010000012
'0' = 4810 = 32+16 = 25+24 = 00110000
Binær til ASCII tekstkonverteringstabell
| Heksadesimal | Binær | ASCII-karakter |
|---|---|---|
| 00 | 00000000 | NUL |
| 01 | 00000001 | SOH |
| 02 | 00000010 | STX |
| 03 | 00000011 | ETX |
| 04 | 00000100 | EOT |
| 05 | 00000101 | ENQ |
| 06 | 00000110 | ACK |
| 07 | 00000111 | BEL |
| 08 | 00001000 | BS |
| 09 | 00001001 | HT |
| 0A | 00001010 | LF |
| 0B | 00001011 | VT |
| 0C | 00001100 | FF |
| 0D | 00001101 | CR |
| 0E | 00001110 | SÅ |
| 0F | 00001111 | SI |
| 10 | 00010000 | DLE |
| 11 | 00010001 | DC1 |
| 12 | 00010010 | DC2 |
| 1. 3 | 00010011 | DC3 |
| 14 | 00010100 | DC4 |
| 15 | 00010101 | NAK |
| 16 | 00010110 | SYN |
| 17 | 00010111 | ETB |
| 18 | 00011000 | KAN |
| 19 | 00011001 | EM |
| 1A | 00011010 | UNDER |
| 1B | 00011011 | ESC |
| 1C | 00011100 | FS |
| 1D | 00011101 | GS |
| 1E | 00011110 | RS |
| 1F | 00011111 | OSS |
| 20 | 00100000 | Rom |
| 21 | 00100001 | ! |
| 22 | 00100010 | " |
| 23 | 00100011 | # |
| 24 | 00100100 | $ |
| 25 | 00100101 | % |
| 26 | 00100110 | & |
| 27 | 00100111 | ' |
| 28 | 00101000 | ( |
| 29 | 00101001 | ) |
| 2A | 00101010 | * |
| 2B | 00101011 | + |
| 2C | 00101100 | , |
| 2D | 00101101 | - |
| 2E | 00101110 | . |
| 2F | 00101111 | / |
| 30 | 00110000 | 0 |
| 31 | 00110001 | 1 |
| 32 | 00110010 | 2 |
| 33 | 00110011 | 3 |
| 34 | 00110100 | 4 |
| 35 | 00110101 | 5 |
| 36 | 00110110 | 6 |
| 37 | 00110111 | 7 |
| 38 | 00111000 | 8 |
| 39 | 00111001 | 9 |
| 3A | 00111010 | : |
| 3B | 00111011 | ; |
| 3C | 00111100 | < |
| 3D | 00111101 | = |
| 3E | 00111110 | > |
| 3F | 00111111 | ? |
| 40 | 01000000 | @ |
| 41 | 01000001 | EN |
| 42 | 01000010 | B |
| 43 | 01000011 | C |
| 44 | 01000100 | D |
| 45 | 01000101 | E |
| 46 | 01000110 | F |
| 47 | 01000111 | G |
| 48 | 01001000 | H |
| 49 | 01001001 | Jeg |
| 4A | 01001010 | J |
| 4B | 01001011 | K |
| 4C | 01001100 | L |
| 4D | 01001101 | M |
| 4E | 01001110 | N |
| 4F | 01001111 | O |
| 50 | 01010000 | P |
| 51 | 01010001 | Q |
| 52 | 01010010 | R |
| 53 | 01010011 | S |
| 54 | 01010100 | T |
| 55 | 01010101 | U |
| 56 | 01010110 | V |
| 57 | 01010111 | W |
| 58 | 01011000 | X |
| 59 | 01011001 | Y |
| 5A | 01011010 | Z |
| 5B | 01011011 | [ |
| 5C | 01011100 | \ |
| 5D | 01011101 | ] |
| 5E | 01011110 | ^ |
| 5F | 01011111 | _ |
| 60 | 01100000 | ` |
| 61 | 01100001 | en |
| 62 | 01100010 | b |
| 63 | 01100011 | c |
| 64 | 01100100 | d |
| 65 | 01100101 | e |
| 66 | 01100110 | f |
| 67 | 01100111 | g |
| 68 | 01101000 | h |
| 69 | 01101001 | Jeg |
| 6A | 01101010 | j |
| 6B | 01101011 | k |
| 6C | 01101100 | l |
| 6D | 01101101 | m |
| 6E | 01101110 | n |
| 6F | 01101111 | o |
| 70 | 01110000 | s |
| 71 | 01110001 | q |
| 72 | 01110010 | r |
| 73 | 01110011 | s |
| 74 | 01110100 | t |
| 75 | 01110101 | u |
| 76 | 01110110 | v |
| 77 | 01110111 | w |
| 78 | 01111000 | x |
| 79 | 01111001 | y |
| 7A | 01111010 | z |
| 7B | 01111011 | { |
| 7C | 01111100 | | |
| 7D | 01111101 | } |
| 7E | 01111110 | ~ |
| 7F | 01111111 | DEL |
Binært system
Det binære tallsystemet bruker tallet 2 som sin base (radix). Som et base-2 tallsystem består det av bare to tall: 0 og 1.
Mens det har blitt brukt i det gamle Egypt, Kina og India for forskjellige formål, har det binære systemet blitt språket for elektronikk og datamaskiner i den moderne verden. Dette er det mest effektive systemet for å oppdage et elektrisk signals av (0) og på (1) tilstand. Det er også grunnlaget for binær kode som brukes til å komponere data i datamaskinbaserte maskiner. Selv den digitale teksten du leser akkurat nå består av binære tall.
ASCII-tekst
ASCII (American Standard Code for Information Interchange) er en av de vanligste standardene for tegnkoding. Opprinnelig utviklet fra telegrafiske koder, er ASCII nå mye brukt i elektronisk kommunikasjon for å formidle tekst.
Den originale ASCII er basert på 128 tegn. Dette er de 26 bokstavene i det engelske alfabetet (både i små og store bokstaver); tall fra 0 til 9; og ulike skilletegn. I ASCII-koden er hvert av disse tegnene tildelt et desimaltall fra 0 til 127. For eksempel er ASCII-representasjonen av store bokstaver A 65 og små bokstaver a er 97.