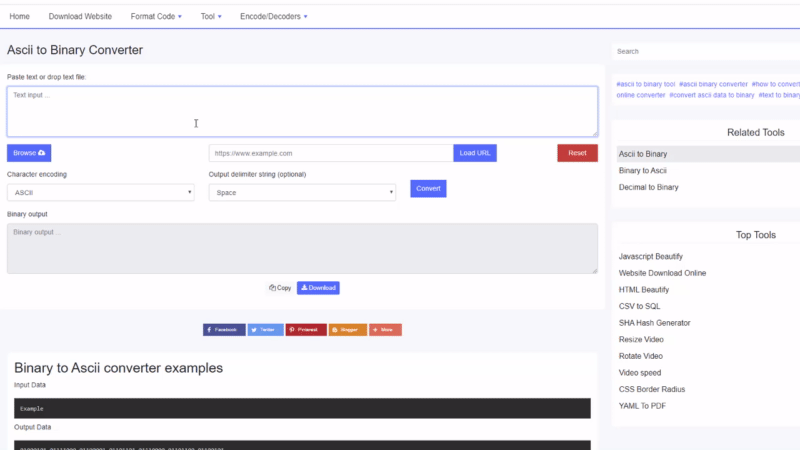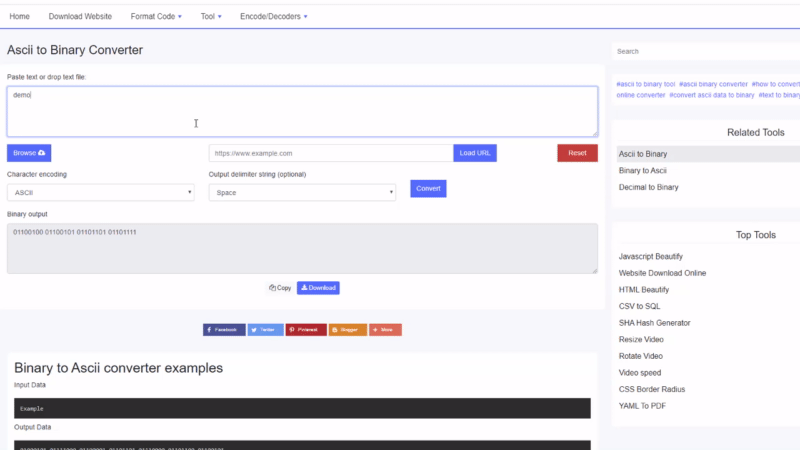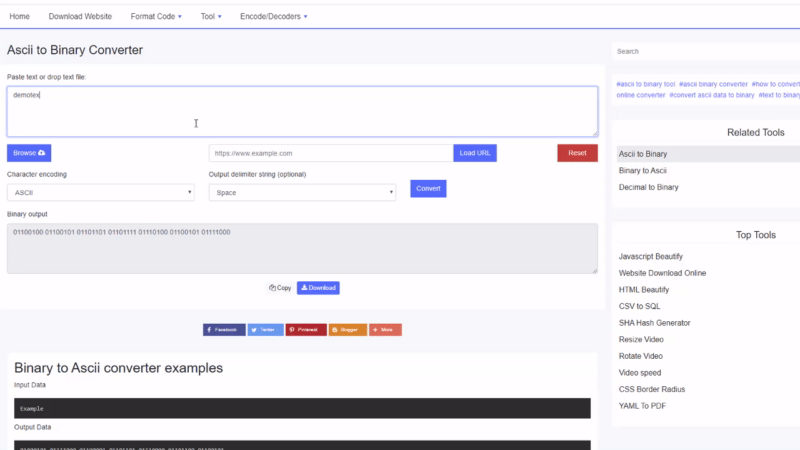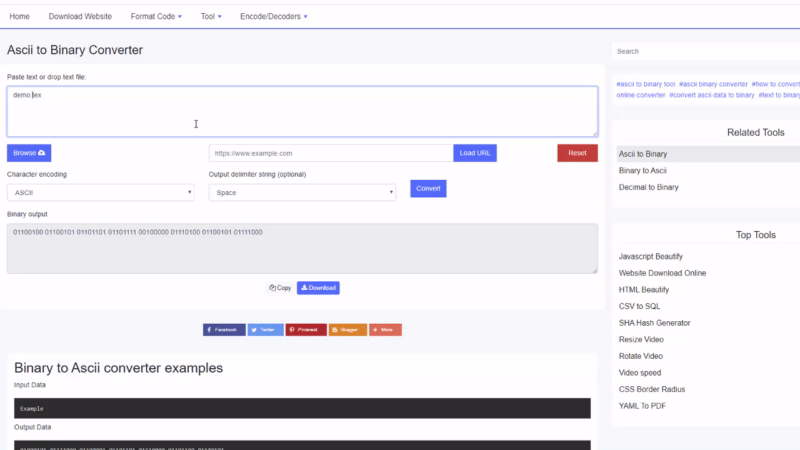
Voorbeelden van binaire naar Ascii-converters
Invoergegevens
ExampleUitvoer gegevens
01000101 01111000 01100001 01101101 01110000 01101100 01100101Hoe binair naar tekst te converteren
Converteer tekst naar binaire ASCII-code:
- Krijg karakter
- Ontvang een decimale tekencode uit de ASCII-tabel
- Converteer decimaal naar binair byte
- Ga verder met het volgende teken
Hoe 01000001 binair naar tekst converteren?
Gebruik ASCII-tabel:
"P" => 80 = 26+24 = 010100002
"l" => 108 = 26+25+23+22 = 011011002
"a" => 97 = 26+25+20 = 011000012
'A' = 6510 = 64+1 = 26+20 = 010000012
'0' = 4810 = 32+16 = 25+24 = 00110000
Binaire naar ASCII-tekstconversietabel
| Hexadecimaal | Binair | ASCII-teken |
|---|---|---|
| 00 | 00000000 | NUL |
| 01 | 00000001 | ZO |
| 02 | 00000010 | STX |
| 03 | 00000011 | ETX |
| 04 | 00000100 | EOT |
| 05 | 00000101 | NLQ |
| 06 | 00000110 | AK |
| 07 | 00000111 | BEL |
| 08 | 00001000 | BS |
| 09 | 00001001 | HT |
| 0A | 00001010 | LF |
| 0B | 00001011 | VT |
| 0C | 00001100 | FF |
| 0D | 00001101 | CR |
| 0E | 00001110 | DUS |
| 0F | 00001111 | SI |
| 10 | 00010000 | DLE |
| 11 | 00010001 | DC1 |
| 12 | 00010010 | DC2 |
| 13 | 00010011 | DC3 |
| 14 | 00010100 | DC4 |
| 15 | 00010101 | NAK |
| 16 | 00010110 | SYN |
| 17 | 00010111 | ETB |
| 18 | 00011000 | KAN |
| 19 | 00011001 | EM |
| 1A | 00011010 | SUB |
| 1B | 00011011 | ESC |
| 1C | 00011100 | FS |
| 1D | 00011101 | GS |
| 1E | 00011110 | RS |
| 1F | 00011111 | ONS |
| 20 | 00100000 | Ruimte |
| 21 | 00100001 | ! |
| 22 | 00100010 | " |
| 23 | 00100011 | # |
| 24 | 00100100 | $ |
| 25 | 00100101 | % |
| 26 | 00100110 | & |
| 27 | 00100111 | ' |
| 28 | 00101000 | ( |
| 29 | 00101001 | ) |
| 2A | 00101010 | * |
| 2B | 00101011 | + |
| 2C | 00101100 | , |
| 2D | 00101101 | - |
| 2E | 00101110 | . |
| 2F | 00101111 | / |
| 30 | 00110000 | 0 |
| 31 | 00110001 | 1 |
| 32 | 00110010 | 2 |
| 33 | 00110011 | 3 |
| 34 | 00110100 | 4 |
| 35 | 00110101 | 5 |
| 36 | 00110110 | 6 |
| 37 | 00110111 | 7 |
| 38 | 00111000 | 8 |
| 39 | 00111001 | 9 |
| 3A | 00111010 | : |
| 3B | 00111011 | ; |
| 3C | 00111100 | < |
| 3D | 00111101 | = |
| 3E | 00111110 | > |
| 3F | 00111111 | ? |
| 40 | 01000000 | @ |
| 41 | 01000001 | A |
| 42 | 01000010 | B |
| 43 | 01000011 | C |
| 44 | 01000100 | D |
| 45 | 01000101 | E |
| 46 | 01000110 | F |
| 47 | 01000111 | G |
| 48 | 01001000 | H |
| 49 | 01001001 | I |
| 4A | 01001010 | J |
| 4B | 01001011 | K |
| 4C | 01001100 | L |
| 4D | 01001101 | M |
| 4E | 01001110 | N |
| 4F | 01001111 | O |
| 50 | 01010000 | P |
| 51 | 01010001 | Q |
| 52 | 01010010 | R |
| 53 | 01010011 | S |
| 54 | 01010100 | T |
| 55 | 01010101 | U |
| 56 | 01010110 | V |
| 57 | 01010111 | W |
| 58 | 01011000 | X |
| 59 | 01011001 | Y |
| 5A | 01011010 | Z |
| 5B | 01011011 | [ |
| 5C | 01011100 | \ |
| 5D | 01011101 | ] |
| 5E | 01011110 | ^ |
| 5F | 01011111 | _ |
| 60 | 01100000 | ` |
| 61 | 01100001 | A |
| 62 | 01100010 | B |
| 63 | 01100011 | C |
| 64 | 01100100 | D |
| 65 | 01100101 | e |
| 66 | 01100110 | F |
| 67 | 01100111 | G |
| 68 | 01101000 | H |
| 69 | 01101001 | i |
| 6A | 01101010 | J |
| 6B | 01101011 | k |
| 6C | 01101100 | ik |
| 6D | 01101101 | M |
| 6E | 01101110 | N |
| 6F | 01101111 | O |
| 70 | 01110000 | P |
| 71 | 01110001 | Q |
| 72 | 01110010 | R |
| 73 | 01110011 | S |
| 74 | 01110100 | T |
| 75 | 01110101 | u |
| 76 | 01110110 | v |
| 77 | 01110111 | w |
| 78 | 01111000 | X |
| 79 | 01111001 | j |
| 7A | 01111010 | z |
| 7B | 01111011 | { |
| 7C | 01111100 | | |
| 7D | 01111101 | } |
| 7E | 01111110 | ~ |
| 7F | 01111111 | DEL |
Binair systeem
Het binaire cijfersysteem gebruikt het getal 2 als grondtal (radix). Als een cijfersysteem met grondtal 2 bestaat het uit slechts twee cijfers: 0 en 1.
Hoewel het in het oude Egypte, China en India voor verschillende doeleinden werd toegepast, is het binaire systeem de taal geworden van elektronica en computers in de moderne wereld. Dit is het meest efficiënte systeem om de uit (0) en aan (1) status van een elektrisch signaal te detecteren. Het is ook de basis voor binaire code die wordt gebruikt om gegevens samen te stellen in computergebaseerde machines. Zelfs de digitale tekst die u nu leest, bestaat uit binaire getallen.
ASCII-tekst
ASCII (American Standard Code for Information Interchange) is een van de meest voorkomende tekencoderingsstandaarden. Oorspronkelijk ontwikkeld op basis van telegrafische codes, wordt ASCII nu veel gebruikt in elektronische communicatie voor het overbrengen van tekst.
De originele ASCII is gebaseerd op 128 tekens. Dit zijn de 26 letters van het Engelse alfabet (zowel in hoofdletters als kleine letters); nummers van 0 tot 9; en diverse leestekens. In de ASCII-code wordt aan elk van deze tekens een decimaal getal toegewezen van 0 tot 127. De ASCII-weergave van hoofdletter A is bijvoorbeeld 65 en de kleine letter a is 97.