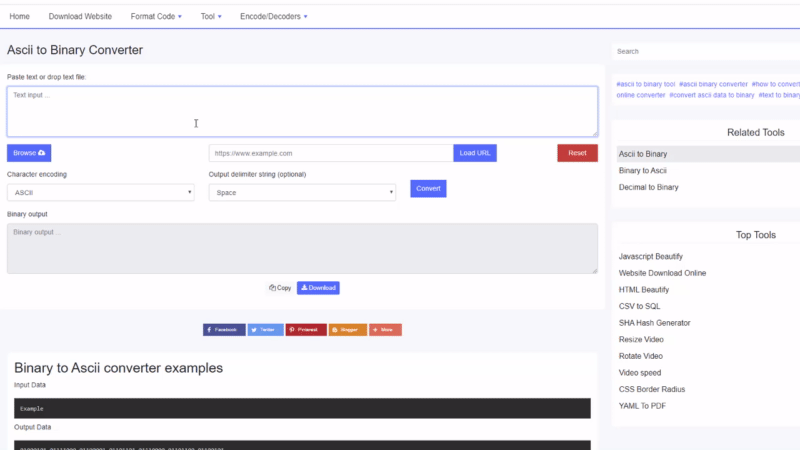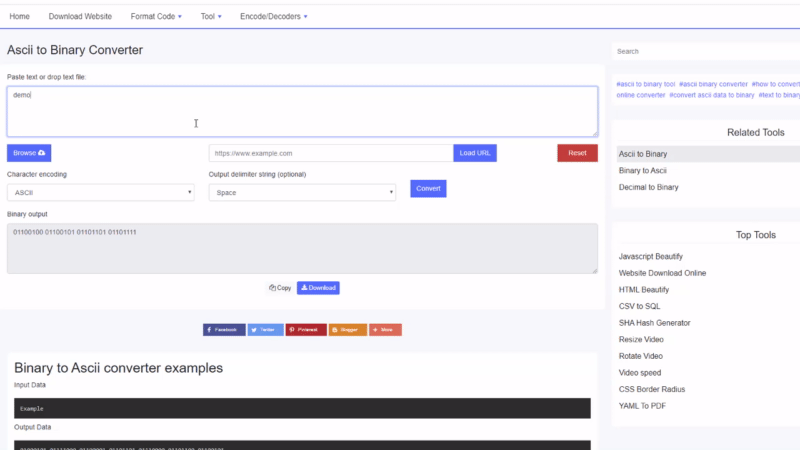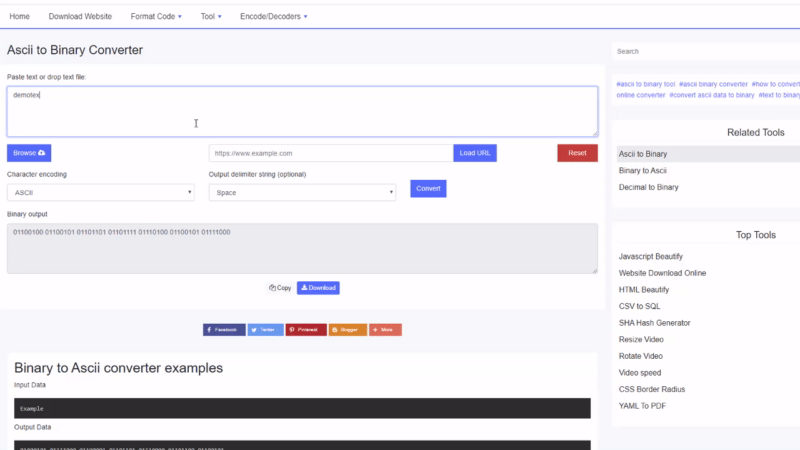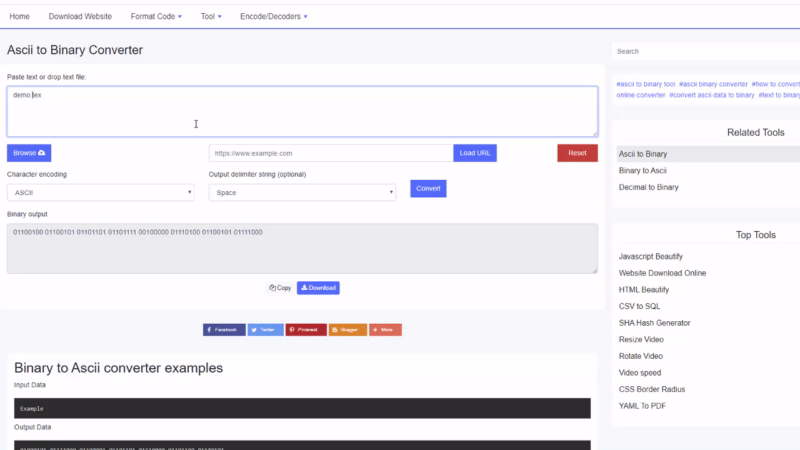
Ascii ტექსტის ორობითი გადამყვანი

Paste text or drop text file

Browse

Character encoding

Output delimiter string (optional)

Binary output

ორობითი რომ Ascii გადამყვანის მაგალითები

Შესაყვანი მონაცემები

Example

გამომავალი მონაცემები

01000101 01111000 01100001 01101101 01110000 01101100 01100101

როგორ გადავიტანოთ ორობითი ტექსტად

ტექსტის გადაქცევა ორობით ASCII კოდში:

მიიღეთ ხასიათი
მიიღეთ სიმბოლოების ათობითი კოდი ASCII ცხრილიდან
ათწილადის გადაქცევა ორობით ბაიტად
გააგრძელეთ შემდეგი პერსონაჟით

როგორ გადავიტანოთ 01000001 ორობითი ტექსტად?

გამოიყენეთ ASCII ცხრილი:

"P" => 80 = 26+24 = 010100002

"l" => 108 = 26+25+23+22 = 011011002

"a" => 97 = 26+25+20 = 011000012

'A' = 6510 = 64+1 = 26+20 = 010000012

'0' = 4810 = 32+16 = 25+24 = 00110000

ორობითი ASCII ტექსტის კონვერტაციის ცხრილი

თექვსმეტობითი	ორობითი	ASCII პერსონაჟი
00	00000000	NUL
01	00000001	SOH
02	00000010	STX
03	00000011	ETX
04	00000100	EOT
05	00000101	ENQ
06	00000110	ACK
07	00000111	BEL
08	00001000	BS
09	00001001	HT
0A	00001010	LF
0B	00001011	VT
0C	00001100	FF
0D	00001101	CR
0E	00001110	ᲘᲡᲔ
0F	00001111	SI
10	00010000	DLE
11	00010001	DC1
12	00010010	DC2
13	00010011	DC3
14	00010100	DC4
15	00010101	NAK
16	00010110	SYN
17	00010111	ETB
18	00011000	შეუძლია
19	00011001	EM
1A	00011010	SUB
1ბ	00011011	ESC
1C	00011100	FS
1D	00011101	გს
1E	00011110	რს
1F	00011111	ᲩᲕᲔᲜ
20	00100000	სივრცე
21	00100001	!
22	00100010	"
23	00100011	#
24	00100100	$
25	00100101	%
26	00100110	&
27	00100111	'
28	00101000	(
29	00101001	)
2A	00101010	*
2ბ	00101011	+
2C	00101100	,
2D	00101101	-
2E	00101110	.
2F	00101111	/
30	00110000	0
31	00110001	1
32	00110010	2
33	00110011	3
34	00110100	4
35	00110101	5
36	00110110	6
37	00110111	7
38	00111000	8
39	00111001	9
3A	00111010	:
3ბ	00111011	;
3C	00111100	<
3D	00111101	=
3E	00111110	>
3F	00111111	?
40	01000000	@
41	01000001	ა
42	01000010	ბ
43	01000011	C
44	01000100	დ
45	01000101	ე
46	01000110	ფ
47	01000111	გ
48	01001000	ჰ
49	01001001	მე
4A	01001010	ჯ
4B	01001011	კ
4C	01001100	ლ
4D	01001101	მ
4E	01001110	ნ
4F	01001111	ო
50	01010000	პ
51	01010001	ქ
52	01010010	რ
53	01010011	ს
54	01010100	თ
55	01010101	უ
56	01010110	ვ
57	01010111	ვ
58	01011000	X
59	01011001	ი
5A	01011010	ზ
5ბ	01011011	[
5C	01011100	\
5D	01011101	]
5E	01011110	^
5F	01011111	_
60	01100000	`
61	01100001	ა
62	01100010	ბ
63	01100011	გ
64	01100100	დ
65	01100101	ე
66	01100110	ვ
67	01100111	გ
68	01101000	თ
69	01101001	მე
6A	01101010	ჯ
6ბ	01101011	კ
6C	01101100	ლ
6D	01101101	მ
6E	01101110	ნ
6F	01101111	ო
70	01110000	გვ
71	01110001	ქ
72	01110010	რ
73	01110011	ს
74	01110100	ტ
75	01110101	u
76	01110110	ვ
77	01110111	ვ
78	01111000	x
79	01111001	წ
7A	01111010	ზ
7ბ	01111011	{
7C	01111100	\|
7D	01111101	}
7E	01111110	~
7F	01111111	DEL

ორობითი სისტემა

ორობითი რიცხვითი სისტემა იყენებს რიცხვ 2-ს, როგორც მის ბაზას (რადიქსი). როგორც საბაზო-2 რიცხვითი სისტემა, იგი შედგება მხოლოდ ორი რიცხვისგან: 0 და 1.

მიუხედავად იმისა, რომ იგი გამოიყენებოდა ძველ ეგვიპტეში, ჩინეთსა და ინდოეთში სხვადასხვა მიზნებისთვის, ბინარული სისტემა გახდა ელექტრონიკის და კომპიუტერების ენა თანამედროვე მსოფლიოში. ეს არის ყველაზე ეფექტური სისტემა ელექტრო სიგნალის გამორთვის (0) და ჩართული (1) მდგომარეობის დასადგენად. ის ასევე არის ორობითი კოდის საფუძველი, რომელიც გამოიყენება კომპიუტერზე დაფუძნებულ მანქანებში მონაცემების შესაქმნელად. ციფრული ტექსტიც კი, რომელსაც ახლა კითხულობთ, შედგება ბინარული რიცხვებისგან.