Esimerkkejä binaari-ascii-muuntimesta
Syöttötiedot
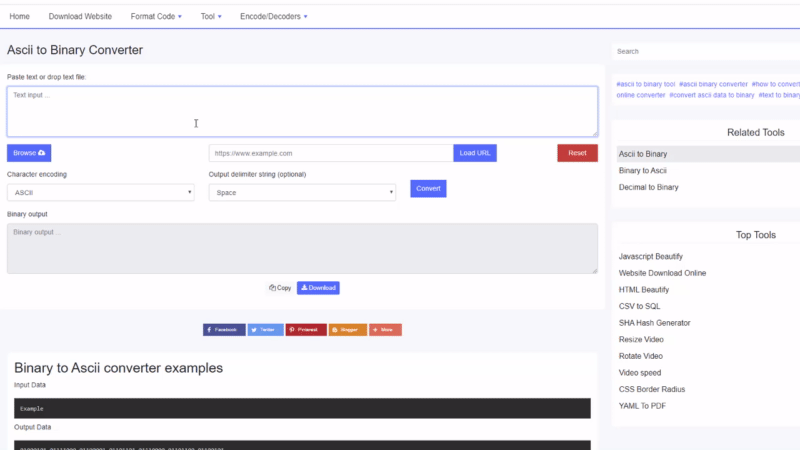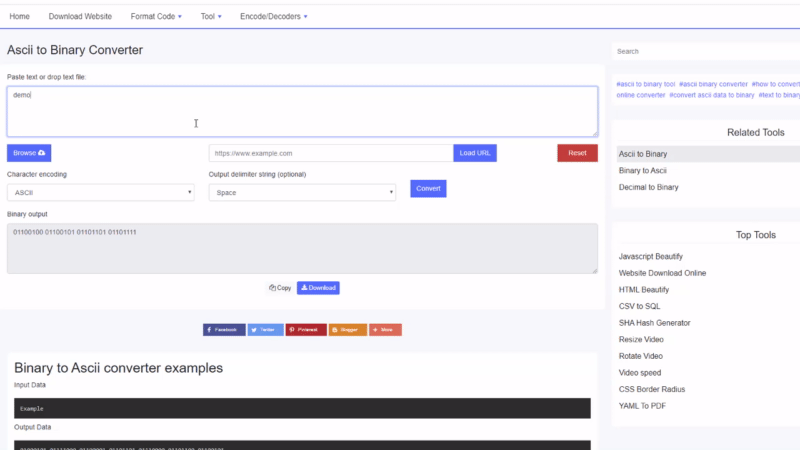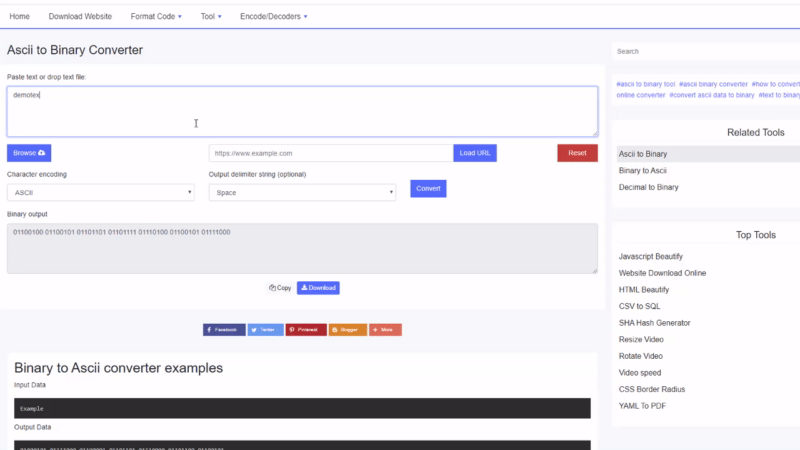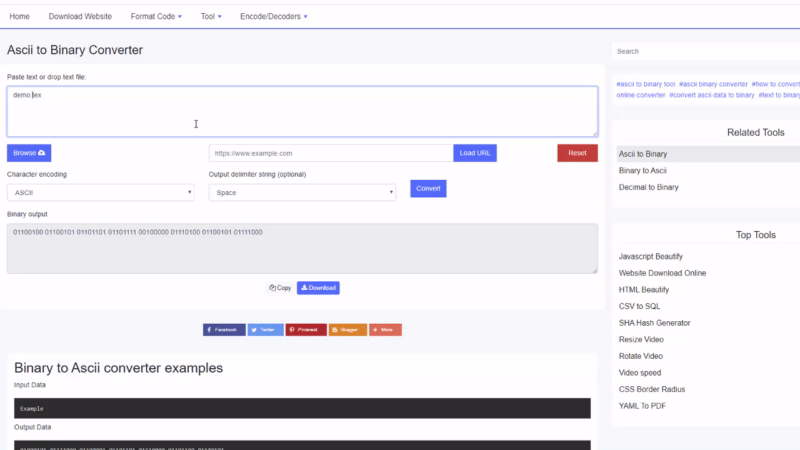
ExampleTulostustiedot
01000101 01111000 01100001 01101101 01110000 01101100 01100101Kuinka muuntaa binaari tekstiksi
Muunna teksti binääriseksi ASCII-koodiksi:
- Hanki luonnetta
- Hae merkin desimaalikoodi ASCII-taulukosta
- Muunna desimaali binääritavuiksi
- Jatka seuraavalla hahmolla
Kuinka muuntaa 01000001 binaari tekstiksi?
Käytä ASCII-taulukkoa:
"P" => 80 = 26+24 = 010100002
"l" => 108 = 26+25+23+22 = 011011002
"a" => 97 = 26+25+20 = 011000012
'A' = 6510 = 64+1 = 26+20 = 010000012
'0' = 4810 = 32+16 = 25+24 = 00110000
Binaari-ASCII-tekstimuunnostaulukko
| Heksadesimaali | Binääri | ASCII-merkki |
|---|---|---|
| 00 | 00000000 | NUL |
| 01 | 00000001 | SOH |
| 02 | 00000010 | STX |
| 03 | 00000011 | ETX |
| 04 | 00000100 | EOT |
| 05 | 00000101 | ENQ |
| 06 | 00000110 | ACK |
| 07 | 00000111 | BEL |
| 08 | 00001000 | BS |
| 09 | 00001001 | HT |
| 0A | 00001010 | LF |
| 0B | 00001011 | VT |
| 0C | 00001100 | FF |
| 0D | 00001101 | CR |
| 0E | 00001110 | NIIN |
| 0F | 00001111 | SI |
| 10 | 00010000 | DLE |
| 11 | 00010001 | DC1 |
| 12 | 00010010 | DC2 |
| 13 | 00010011 | DC3 |
| 14 | 00010100 | DC4 |
| 15 | 00010101 | NAK |
| 16 | 00010110 | SYN |
| 17 | 00010111 | ETB |
| 18 | 00011000 | VOI |
| 19 | 00011001 | EM |
| 1A | 00011010 | SUB |
| 1B | 00011011 | POISTU |
| 1C | 00011100 | FS |
| 1D | 00011101 | GS |
| 1E | 00011110 | RS |
| 1F | 00011111 | MEILLE |
| 20 | 00100000 | Avaruus |
| 21 | 00100001 | ! |
| 22 | 00100010 | " |
| 23 | 00100011 | # |
| 24 | 00100100 | $ |
| 25 | 00100101 | % |
| 26 | 00100110 | & |
| 27 | 00100111 | ' |
| 28 | 00101000 | ( |
| 29 | 00101001 | ) |
| 2A | 00101010 | * |
| 2B | 00101011 | + |
| 2C | 00101100 | , |
| 2D | 00101101 | - |
| 2E | 00101110 | . |
| 2F | 00101111 | / |
| 30 | 00110000 | 0 |
| 31 | 00110001 | 1 |
| 32 | 00110010 | 2 |
| 33 | 00110011 | 3 |
| 34 | 00110100 | 4 |
| 35 | 00110101 | 5 |
| 36 | 00110110 | 6 |
| 37 | 00110111 | 7 |
| 38 | 00111000 | 8 |
| 39 | 00111001 | 9 |
| 3A | 00111010 | : |
| 3B | 00111011 | ; |
| 3C | 00111100 | < |
| 3D | 00111101 | = |
| 3E | 00111110 | > |
| 3F | 00111111 | ? |
| 40 | 01000000 | @ |
| 41 | 01000001 | A |
| 42 | 01000010 | B |
| 43 | 01000011 | C |
| 44 | 01000100 | D |
| 45 | 01000101 | E |
| 46 | 01000110 | F |
| 47 | 01000111 | G |
| 48 | 01001000 | H |
| 49 | 01001001 | minä |
| 4A | 01001010 | J |
| 4B | 01001011 | K |
| 4C | 01001100 | L |
| 4D | 01001101 | M |
| 4E | 01001110 | N |
| 4F | 01001111 | O |
| 50 | 01010000 | P |
| 51 | 01010001 | K |
| 52 | 01010010 | R |
| 53 | 01010011 | S |
| 54 | 01010100 | T |
| 55 | 01010101 | U |
| 56 | 01010110 | V |
| 57 | 01010111 | W |
| 58 | 01011000 | X |
| 59 | 01011001 | Y |
| 5A | 01011010 | Z |
| 5B | 01011011 | [ |
| 5C | 01011100 | \ |
| 5D | 01011101 | ] |
| 5E | 01011110 | ^ |
| 5F | 01011111 | _ |
| 60 | 01100000 | ` |
| 61 | 01100001 | a |
| 62 | 01100010 | b |
| 63 | 01100011 | c |
| 64 | 01100100 | d |
| 65 | 01100101 | e |
| 66 | 01100110 | f |
| 67 | 01100111 | g |
| 68 | 01101000 | h |
| 69 | 01101001 | i |
| 6A | 01101010 | j |
| 6B | 01101011 | k |
| 6C | 01101100 | l |
| 6D | 01101101 | m |
| 6E | 01101110 | n |
| 6F | 01101111 | o |
| 70 | 01110000 | s |
| 71 | 01110001 | q |
| 72 | 01110010 | r |
| 73 | 01110011 | s |
| 74 | 01110100 | t |
| 75 | 01110101 | u |
| 76 | 01110110 | v |
| 77 | 01110111 | w |
| 78 | 01111000 | x |
| 79 | 01111001 | y |
| 7A | 01111010 | z |
| 7B | 01111011 | { |
| 7C | 01111100 | | |
| 7D | 01111101 | } |
| 7E | 01111110 | ~ |
| 7F | 01111111 | DEL |
Binäärijärjestelmä
Binäärilukujärjestelmä käyttää lukua 2 kantalukunaan. 2-kantaisena numerojärjestelmänä se koostuu vain kahdesta numerosta: 0 ja 1.
Vaikka sitä on käytetty muinaisessa Egyptissä, Kiinassa ja Intiassa eri tarkoituksiin, binäärijärjestelmästä on tullut elektroniikan ja tietokoneiden kieli nykymaailmassa. Tämä on tehokkain järjestelmä sähköisen signaalin pois (0) ja päällä (1) tilan havaitsemiseen. Se on myös perusta binäärikoodille, jota käytetään tietojen muodostamiseen tietokonepohjaisissa koneissa. Jopa digitaalinen teksti, jota luet juuri nyt, koostuu binääriluvuista.
ASCII-teksti
ASCII (American Standard Code for Information Interchange) on yksi yleisimmistä merkkikoodausstandardeista. Alun perin sähkekoodeista kehitetty ASCII on nykyään laajalti käytössä sähköisessä viestinnässä tekstin välittämiseen.
Alkuperäinen ASCII perustuu 128 merkkiin. Nämä ovat englannin aakkosten 26 kirjainta (sekä pienillä että isoilla kirjaimilla); numerot 0-9; ja erilaisia välimerkkejä. ASCII-koodissa kullekin näistä merkeistä on määritetty desimaaliluku väliltä 0–127. Esimerkiksi isojen kirjainten A ASCII-esitys on 65 ja pienten kirjainten a 97.