Convertisseur décimal en binaire

Comment convertir décimal en binaire

Étapes de conversion :

  1. Divisez le nombre par 2.
  2. Obtenez le quotient entier pour la prochaine itération.
  3. Obtenez le reste du chiffre binaire.
  4. Répétez les étapes jusqu'à ce que le quotient soit égal à 0.

Exemple 1

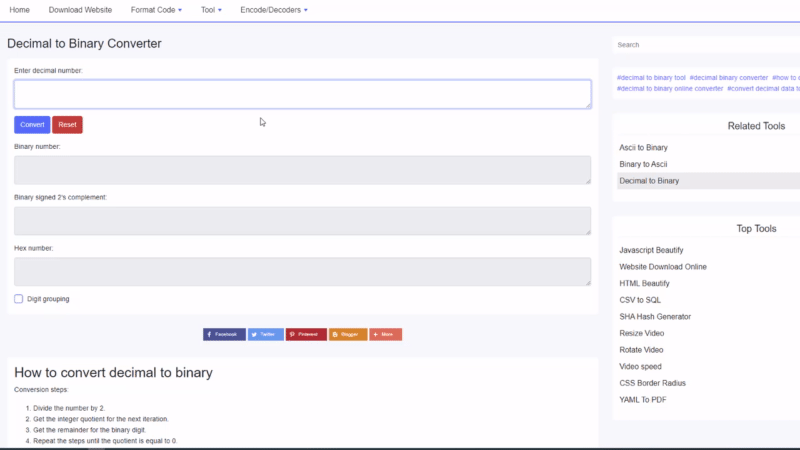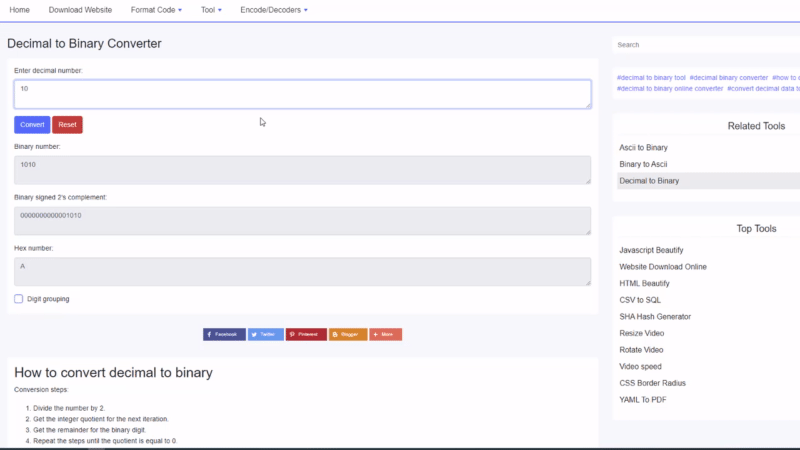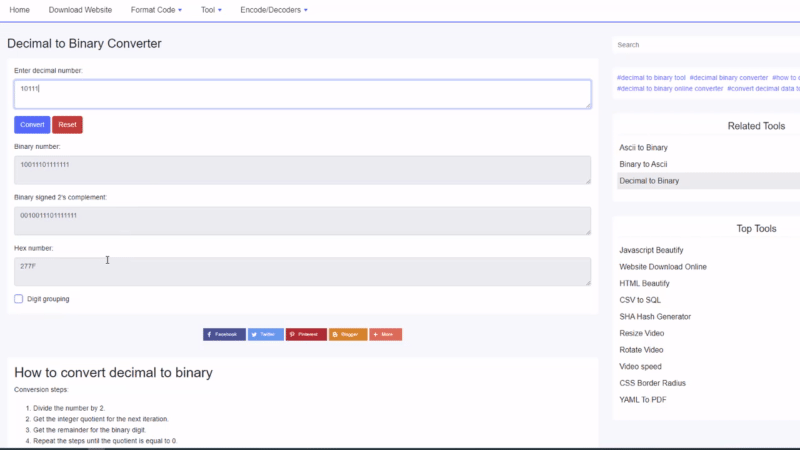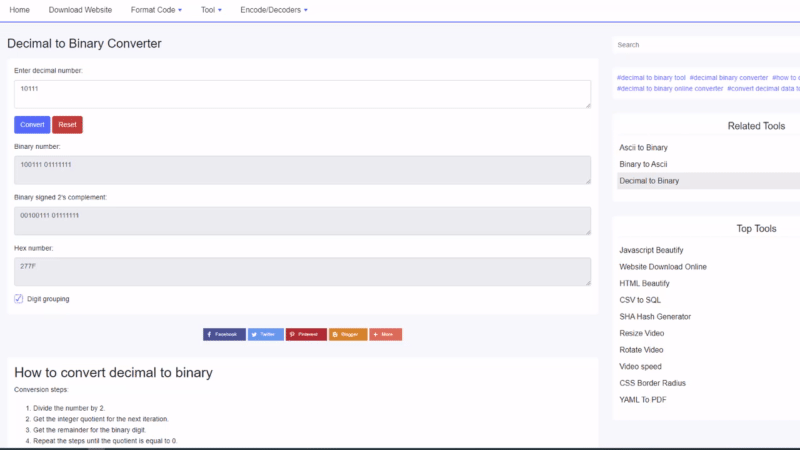
Convertir 41 10  en binaire :

Division par 2 Quotient Reste Bit #
41/2 20 1 0
20/2 dix 0 1
10/2 5 0 2
5/2 2 1 3
2/2 1 0 4
1/2 0 1 5

Donc 41 10 = 101001 2

Tableau de conversion décimal en binaire

Nombre décimal Nombre binaire Numéro hexadécimal
0 0 0
1 1 1
2 dix 2
3 11 3
4 100 4
5 101 5
6 110 6
7 111 7
8 1000 8
9 1001 9
dix 1010 UNE
11 1011 B
12 1100 C
13 1101 ré
14 1110 E
15 1111 F
16 10000 dix
17 10001 11
18 10010 12
19 10011 13
20 10100 14
21 10101 15
22 10110 16
23 10111 17
24 11000 18
25 11001 19
26 11010 1A
27 11011 1B
28 11100 1C
29 11101 1D
30 11110 1E
31 11111 1F
32 100000 20
64 1000000 40
128 10000000 80
256 100000000 100

Système décimal

Le système de nombres décimaux est le système le plus couramment utilisé et le système standard dans la vie quotidienne. Il utilise le nombre 10 comme base (radix). Par conséquent, il a 10 symboles : Les nombres de 0 à 9 ; à savoir 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.

Système binaire

Le système de numération binaire utilise le nombre 2 comme base (base). En tant que système numérique de base 2, il se compose de seulement deux nombres : 0 et 1.