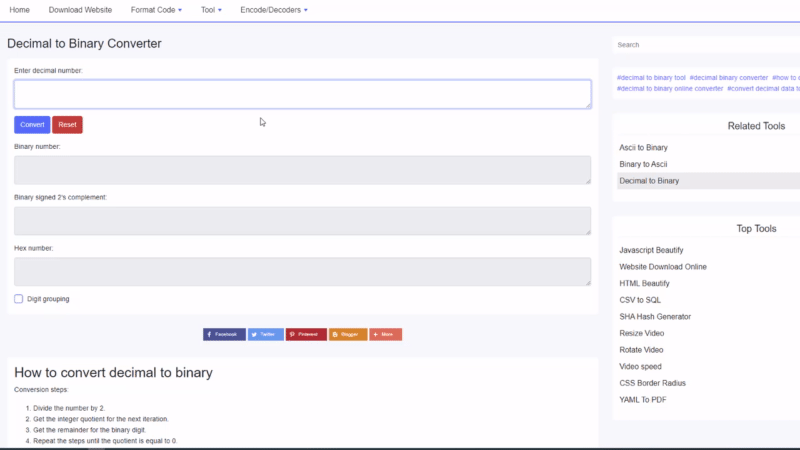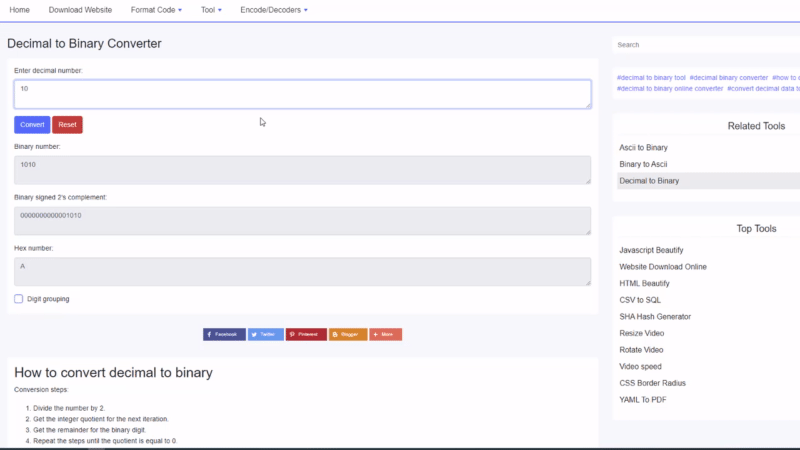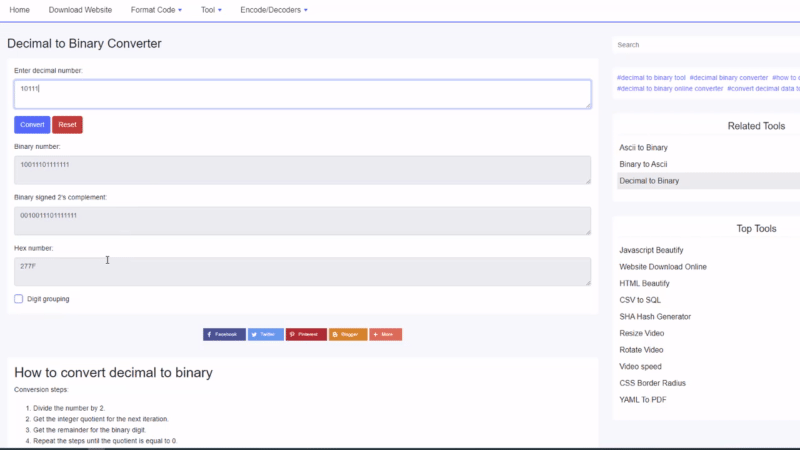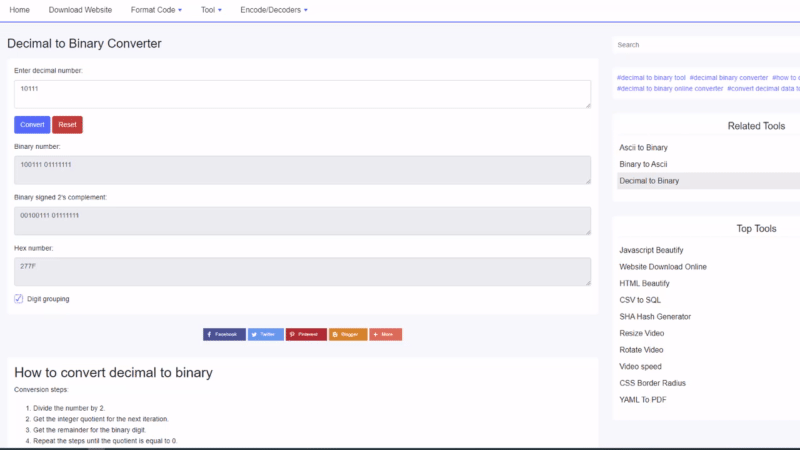
Convertitore da decimale a binario

Come convertire decimale in binario

Passaggi di conversione:

  1. Dividi il numero per 2.
  2. Ottieni il quoziente intero per l'iterazione successiva.
  3. Ottieni il resto per la cifra binaria.
  4. Ripetere i passaggi fino a quando il quoziente è uguale a 0.

Esempio 1

Converti 41 10  in binario:

Divisione per 2 Quoziente Resto Po #
41/2 20 1 0
20/2 10 0 1
10/2 5 0 2
5/2 2 1 3
2/2 1 0 4
1/2 0 1 5

Quindi 41 10 = 101001 2

Tabella di conversione da decimale a binario

Numero decimale Numero binario Numero esadecimale
0 0 0
1 1 1
2 10 2
3 11 3
4 100 4
5 101 5
6 110 6
7 111 7
8 1000 8
9 1001 9
10 1010 UN
11 1011 B
12 1100 C
13 1101 D
14 1110 E
15 1111 F
16 10000 10
17 10001 11
18 10010 12
19 10011 13
20 10100 14
21 10101 15
22 10110 16
23 10111 17
24 11000 18
25 11001 19
26 11010 1A
27 11011 1B
28 11100 1C
29 11101 1D
30 11110 1E
31 11111 1F
32 100000 20
64 1000000 40
128 10000000 80
256 10000000 100

Sistema decimale

Il sistema di numerazione decimale è il più comunemente usato e il sistema standard nella vita quotidiana. Usa il numero 10 come base (radix). Pertanto, ha 10 simboli: i numeri da 0 a 9; vale a dire 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.

Sistema binario

Il sistema numerico binario utilizza il numero 2 come base (radice). Essendo un sistema numerico in base 2, è composto solo da due numeri: 0 e 1.