Cómo convertir binario a decimal
Para números binarios con n dígitos:
d n-1 ... d 3 d 2 d 1 d 0
El número decimal es igual a la suma de dígitos binarios (d n ) por su potencia de 2 (2 n ):
decimal = d 0 × 2 0 + d 1 × 2 1 + d 2 × 2 2 + ...
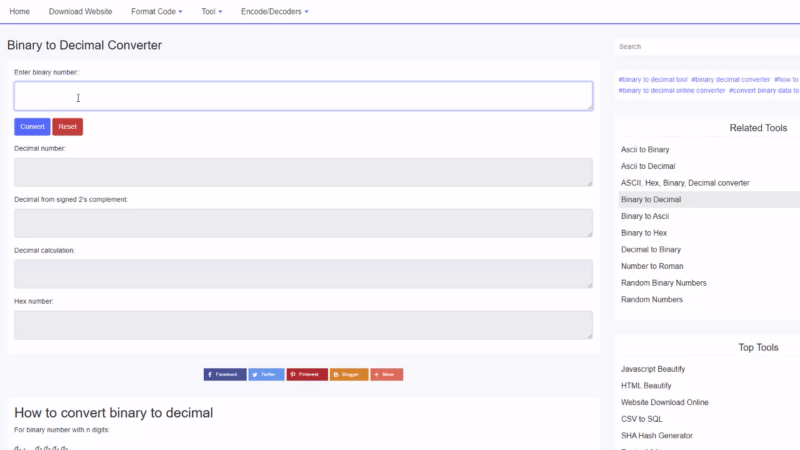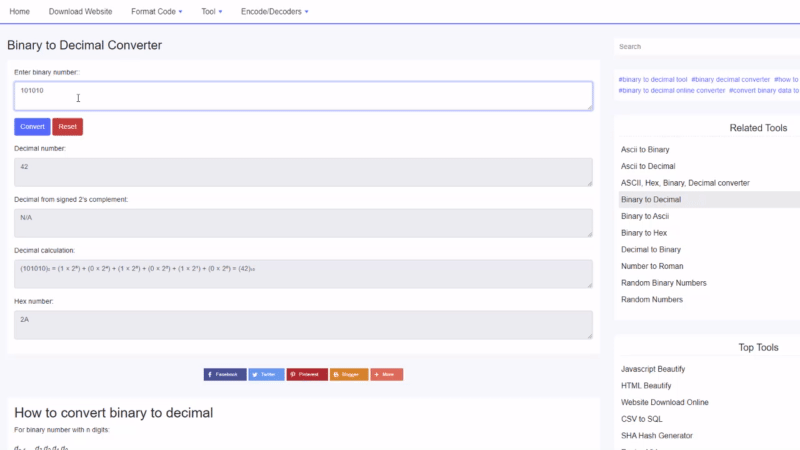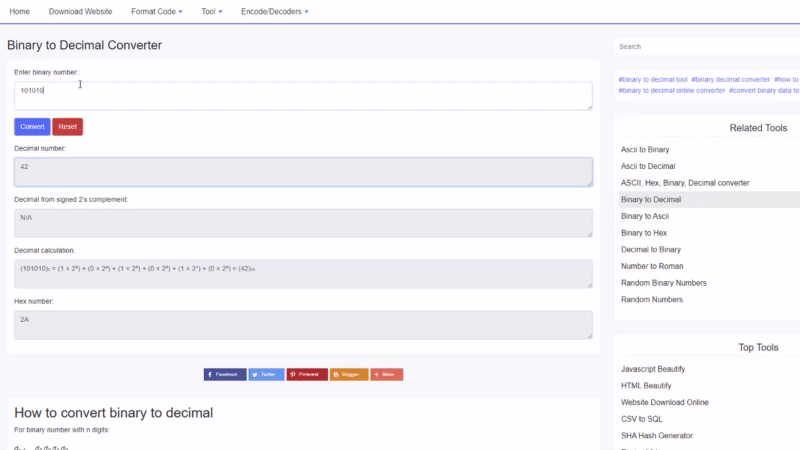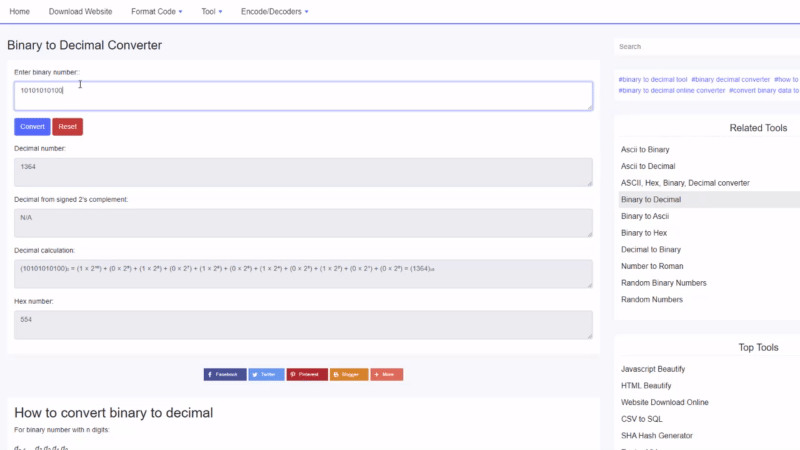
Ejemplo de binario a decimal
Encuentre el valor decimal de 100010 2 :
| número binario: | 1 | 0 | 0 | 0 | 1 | 0 |
|---|---|---|---|---|---|---|
| poder de 2: | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
100010 2 = 1⋅2 5 + 0⋅2 4 + 0⋅2 3 + 0⋅2 2 + 1⋅2 1 + 0⋅2 0 = 34 10
Sistema decimal
El sistema de numeración decimal es el más utilizado y el sistema estándar en la vida diaria. Utiliza el número 10 como base (raíz). Por tanto, tiene 10 símbolos: Los números del 0 al 9; a saber, 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.
Sistema binario
El sistema de numeración binario usa el número 2 como base (raíz). Como sistema numérico de base 2, consta de solo dos números: 0 y 1.
Tabla de conversión de binario a decimal
| Número binario | Número decimal | Número hexadecimal |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | mi |
| 1111 | 15 | F |
| 10000 | dieciséis | 10 |
| 10001 | 17 | 11 |
| 10010 | 18 | 12 |
| 10011 | 19 | 13 |
| 10100 | 20 | 14 |
| 10101 | 21 | 15 |
| 10110 | 22 | dieciséis |
| 10111 | 23 | 17 |
| 11000 | 24 | 18 |
| 11001 | 25 | 19 |
| 11010 | 26 | 1A |
| 11011 | 27 | 1B |
| 11100 | 28 | 1C |
| 11101 | 29 | 1D |
| 11110 | 30 | 1E |
| 11111 | 31 | 1F |
| 100000 | 32 | 20 |
| 1000000 | 64 | 40 |
| 10000000 | 128 | 80 |
| 100000000 | 256 | 100 |