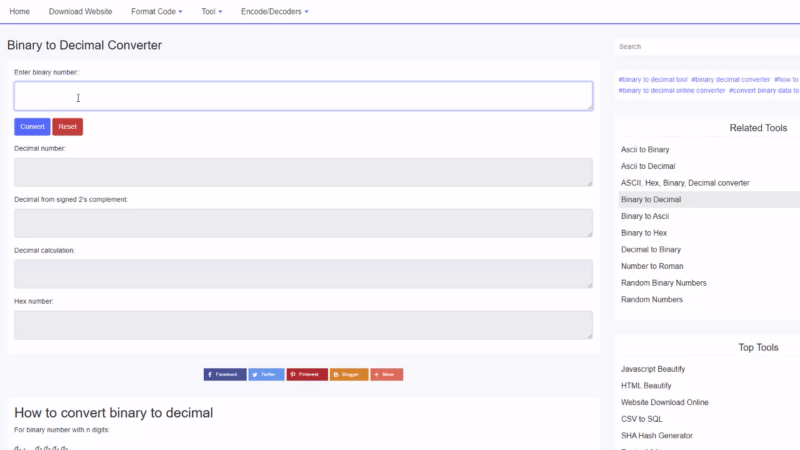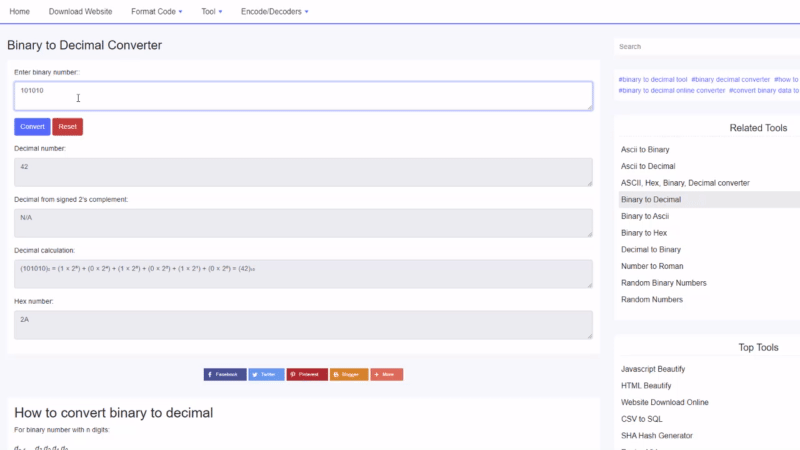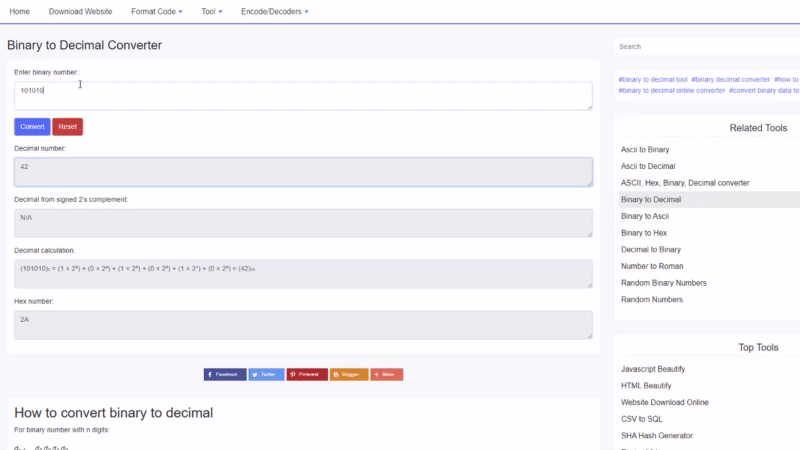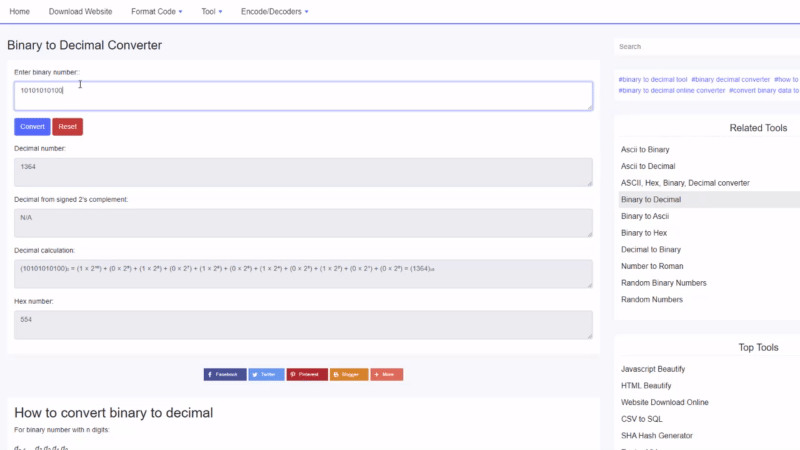
Conas dénártha a thiontú go deachúil
Le haghaidh uimhir dhénártha le n dhigit:
d n-1 ... d 3 d 2 d 1 d 0
Is ionann an uimhir dheachúil agus suim na ndigit dhénártha ( d n ) uair a gcumhacht 2 ( 2 n ):
deachúil = d 0 ×2 0 + d 1 ×2 1 + d 2 ×2 2 + ...
Sampla Dénártha go Deachúil
Faigh an luach deachúil ar 100010 2 :
| uimhir dhénártha: | 1 | 0 | 0 | 0 | 1 | 0 |
|---|---|---|---|---|---|---|
| cumhacht 2: | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
100010 2 = 1⋅2 5 +0⋅2 4 +0⋅2 3 +0⋅2 2 +1⋅2 1 +0⋅2 0 = 34 10
Córas Deachúil
Is é an córas uimhir dheachúil an ceann is coitianta a úsáidtear agus an córas caighdeánach sa saol laethúil. Úsáideann sé an uimhir 10 mar bhonn (radix). Mar sin, tá 10 siombail aige: Na huimhreacha ó 0 go 9; eadhon 0, 1, 2, 3, 4, 5, 6, 7, 8 agus 9.
Córas Dénártha
Úsáideann an córas uimhir dhénártha an uimhir 2 mar bhonn (radics). Mar chóras uimhriúil bonn-2, níl ann ach dhá uimhir: 0 agus 1.
Tábla comhshó dhénártha go deachúla
| Uimhir Dhénártha | Uimhir Dheachúil | Uimhir Heics |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | b |
| 1100 | 12 | c |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
| 10000 | 16 | 10 |
| 10001 | 17 | 11 |
| 10010 | 18 | 12 |
| 10011 | 19 | 13 |
| 10100 | 20 | 14 |
| 10101 | 21 | 15 |
| 10110 | 22 | 16 |
| 10111 | 23 | 17 |
| 11000 | 24 | 18 |
| 11001 | 25 | 19 |
| 11010 | 26 | 1A |
| 11011 | 27 | 1B |
| 11100 | 28 | 1C |
| 11101 | 29 | 1d |
| 11110 | 30 | 1E |
| 11111 | 31 | 1F |
| 100000 | 32 | 20 |
| 1000000 | 64 | 40 |
| 10000000 | 128 | 80 |
| 100000000 | 256 | 100 |