বাইনারি থেকে দশমিক কনভার্টার

কীভাবে বাইনারিকে দশমিকে রূপান্তর করবেন

n সংখ্যা সহ বাইনারি সংখ্যার জন্য:

d n-1  ... d 3  d 2  d 1  d 0

দশমিক সংখ্যাটি বাইনারি ডিজিটের সমষ্টির সমান (d n ) গুণ তাদের 2 (2 n ):

দশমিক =  d 0 × 2 0  +  d 1 × 2 1  +  d 2 × 2 2  + ...

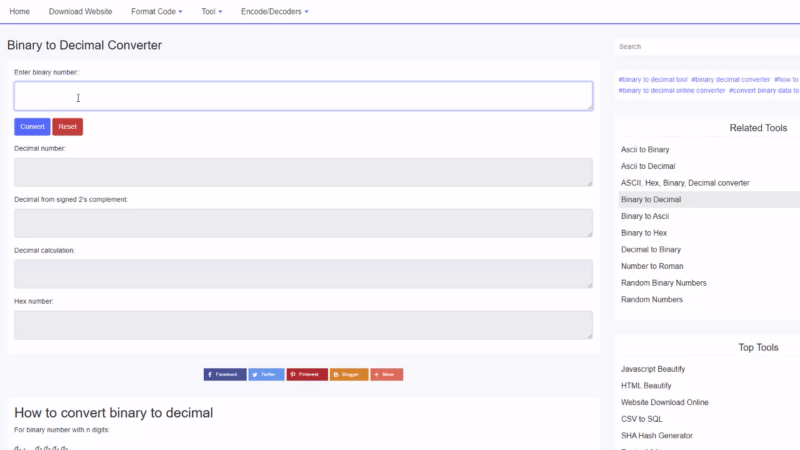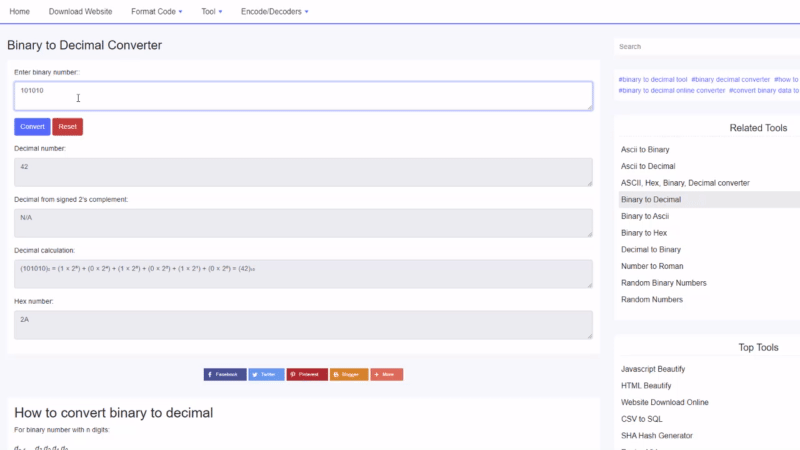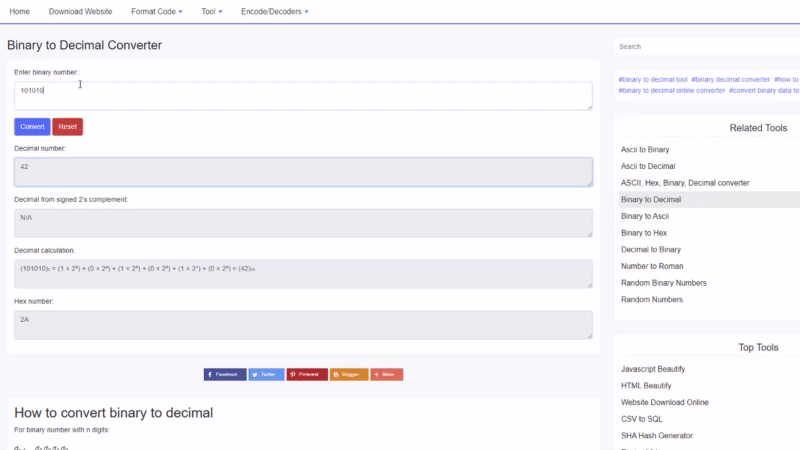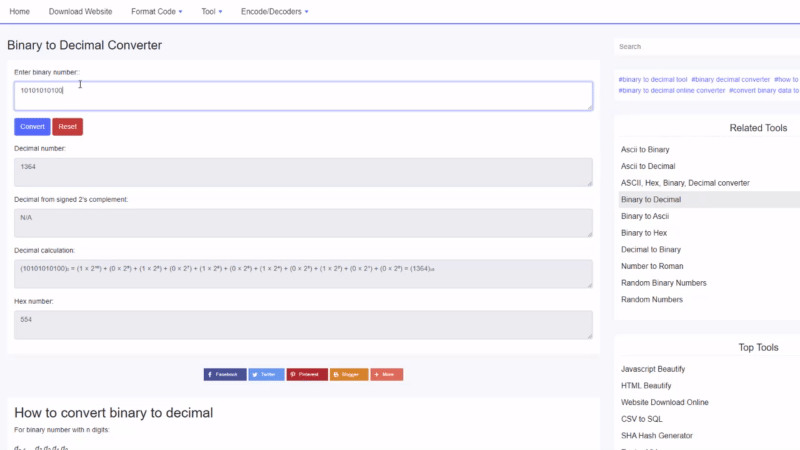
বাইনারি থেকে দশমিক উদাহরণ

100010 2 এর দশমিক মান খুঁজুন :

বাইনারি সংখ্যা: 1 0 0 0 1 0
2 এর শক্তি: 2 5 2 4 2 3 2 2 2 1 2 0

100010 2  = 1⋅2 5 +0⋅2 4 +0⋅2 3 +0⋅2 2 +1⋅2 1 +0⋅2 0 = 34 10

দশমিক সিস্টেম

দশমিক সংখ্যা পদ্ধতি  হল সবচেয়ে বেশি ব্যবহৃত এবং দৈনন্দিন জীবনে আদর্শ সিস্টেম। এটি তার ভিত্তি হিসাবে 10 নম্বর ব্যবহার করে (রেডিক্স)। অতএব, এতে 10টি চিহ্ন রয়েছে: 0 থেকে 9 পর্যন্ত সংখ্যা; যথা 0, 1, 2, 3, 4, 5, 6, 7, 8 এবং 9।

বাইনারি সিস্টেম

বাইনারি সংখ্যা পদ্ধতি  2 সংখ্যাটিকে তার ভিত্তি হিসাবে ব্যবহার করে (র্যাডিক্স)। একটি বেস-2 সংখ্যা পদ্ধতি হিসাবে, এটি শুধুমাত্র দুটি সংখ্যা নিয়ে গঠিত: 0 এবং 1। 

বাইনারি থেকে দশমিক রূপান্তর টেবিল

বাইনারি সংখ্যা দশমিক সংখ্যা হেক্স নম্বর
0 0 0
1 1 1
10 2 2
11 3 3
100 4 4
101 5 5
110 6 6
111 7 7
1000 8 8
1001 9 9
1010 10 ক
1011 11 খ
1100 12 গ
1101 13 ডি
1110 14 ই
1111 15 চ
10000 16 10
10001 17 11
10010 18 12
10011 19 13
10100 20 14
10101 21 15
10110 22 16
10111 23 17
11000 24 18
11001 25 19
11010 26 1A
11011 27 1 বি
11100 28 1C
11101 29 1D
11110 30 1ই
11111 31 1F
100000 32 20
1000000 64 40
10000000 128 80
100000000 256 100