ਬਾਈਨਰੀ ਤੋਂ ਦਸ਼ਮਲਵ ਪਰਿਵਰਤਕ

ਬਾਈਨਰੀ ਨੂੰ ਦਸ਼ਮਲਵ ਵਿੱਚ ਕਿਵੇਂ ਬਦਲਿਆ ਜਾਵੇ

n ਅੰਕਾਂ ਵਾਲੇ ਬਾਈਨਰੀ ਨੰਬਰ ਲਈ:

d n-1  ... d 3  d 2  d 1  d 0

ਦਸ਼ਮਲਵ ਸੰਖਿਆ ਬਾਈਨਰੀ ਅੰਕਾਂ ਦੇ ਜੋੜ (d n ) ਗੁਣਾ ਉਹਨਾਂ ਦੀ 2 (2 n ) ਦੀ ਸ਼ਕਤੀ ਦੇ ਬਰਾਬਰ ਹੈ :

ਦਸ਼ਮਲਵ =  d 0 × 2 0  +  d 1 × 2 1  +  d 2 × 2 2  + ...

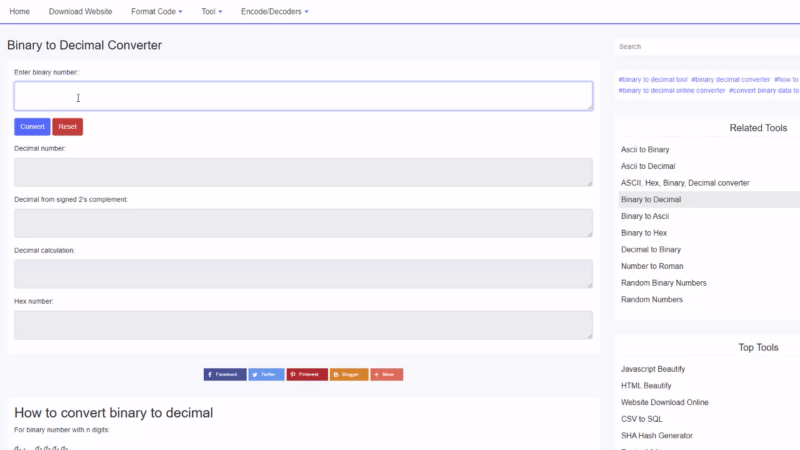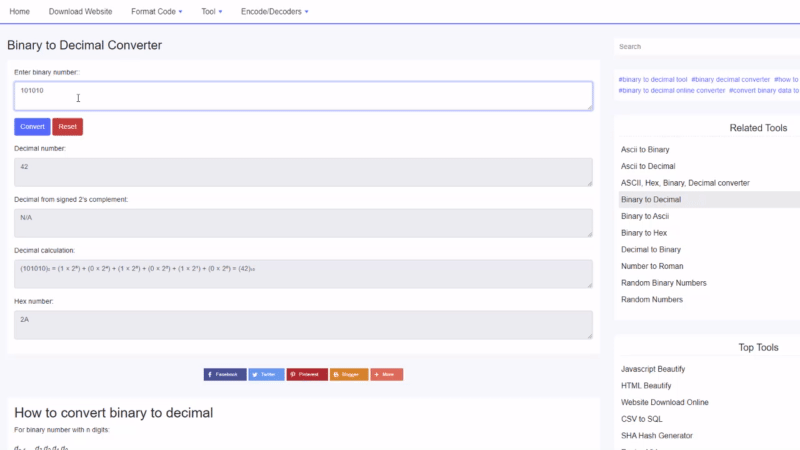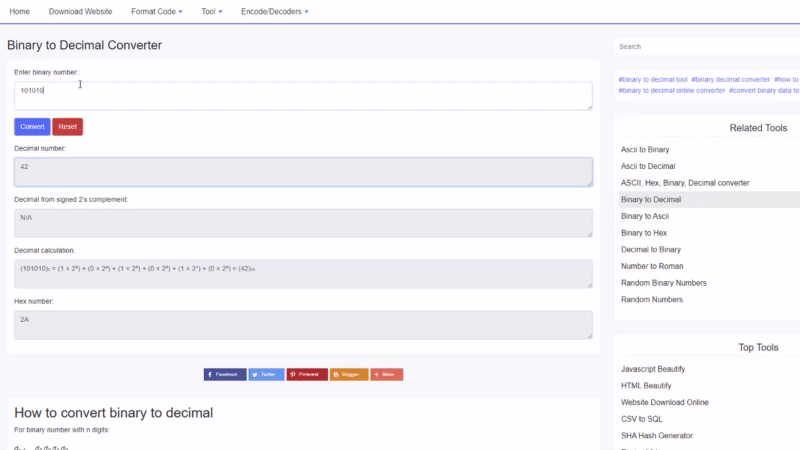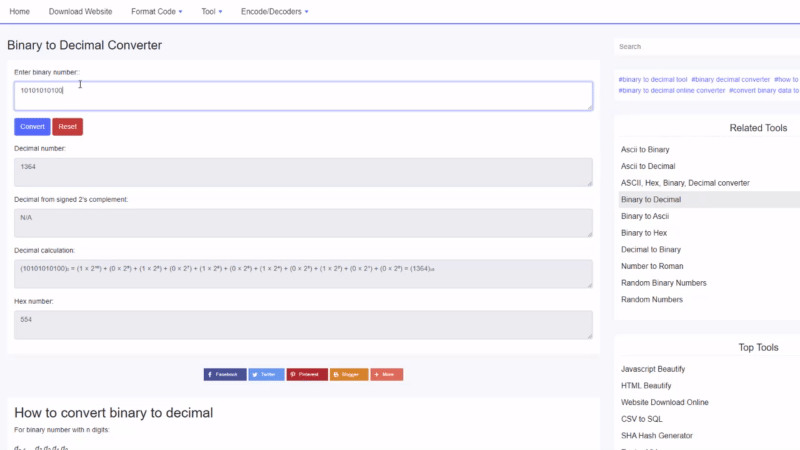
ਬਾਈਨਰੀ ਤੋਂ ਦਸ਼ਮਲਵ ਉਦਾਹਰਨ

100010 2 ਦਾ ਦਸ਼ਮਲਵ ਮੁੱਲ ਲੱਭੋ :

ਬਾਈਨਰੀ ਨੰਬਰ: 1 0 0 0 1 0
2 ਦੀ ਸ਼ਕਤੀ: 2 5 2 4 2 3 2 2 2 1 2 0

100010 2  = 1⋅2 5 +0⋅2 4 +0⋅2 3 +0⋅2 2 +1⋅2 1 +0⋅2 0 = 34 10

ਦਸ਼ਮਲਵ ਸਿਸਟਮ

ਦਸ਼ਮਲਵ ਸੰਖਿਆ ਪ੍ਰਣਾਲੀ  ਰੋਜ਼ਾਨਾ ਜੀਵਨ ਵਿੱਚ ਸਭ ਤੋਂ ਵੱਧ ਵਰਤੀ ਜਾਂਦੀ ਅਤੇ ਮਿਆਰੀ ਪ੍ਰਣਾਲੀ ਹੈ। ਇਹ ਆਪਣੇ ਅਧਾਰ (ਰੇਡੀਕਸ) ਵਜੋਂ ਨੰਬਰ 10 ਦੀ ਵਰਤੋਂ ਕਰਦਾ ਹੈ। ਇਸ ਲਈ, ਇਸਦੇ 10 ਚਿੰਨ੍ਹ ਹਨ: 0 ਤੋਂ 9 ਤੱਕ ਦੇ ਨੰਬਰ; ਅਰਥਾਤ 0, 1, 2, 3, 4, 5, 6, 7, 8 ਅਤੇ 9।

ਬਾਈਨਰੀ ਸਿਸਟਮ

ਬਾਈਨਰੀ ਸੰਖਿਆ ਪ੍ਰਣਾਲੀ  ਆਪਣੇ ਅਧਾਰ (ਰੇਡੀਕਸ) ਵਜੋਂ ਨੰਬਰ 2 ਦੀ ਵਰਤੋਂ ਕਰਦੀ ਹੈ। ਇੱਕ ਅਧਾਰ-2 ਸੰਖਿਆ ਪ੍ਰਣਾਲੀ ਦੇ ਰੂਪ ਵਿੱਚ, ਇਸ ਵਿੱਚ ਸਿਰਫ ਦੋ ਸੰਖਿਆਵਾਂ ਹਨ: 0 ਅਤੇ 1। 

ਬਾਈਨਰੀ ਤੋਂ ਦਸ਼ਮਲਵ ਰੂਪਾਂਤਰਣ ਸਾਰਣੀ

ਬਾਈਨਰੀ ਨੰਬਰ ਦਸ਼ਮਲਵ ਸੰਖਿਆ ਹੈਕਸ ਨੰਬਰ
0 0 0
1 1 1
10 2 2
11 3 3
100 4 4
101 5 5
110 6 6
111 7 7
1000 8 8
1001 9 9
1010 10 ਏ
1011 11 ਬੀ
1100 12 ਸੀ
1101 13 ਡੀ
1110 14 ਈ
1111 15 ਐੱਫ
10000 16 10
10001 17 11
10010 18 12
10011 19 13
10100 ਹੈ 20 14
10101 21 15
10110 22 16
10111 23 17
11000 24 18
11001 25 19
11010 26 1 ਏ
11011 27 1ਬੀ
11100 ਹੈ 28 1 ਸੀ
11101 29 1 ਡੀ
11110 30 1 ਈ
11111 31 1 ਐੱਫ
100000 32 20
1000000 64 40
10000000 128 80
100000000 256 100