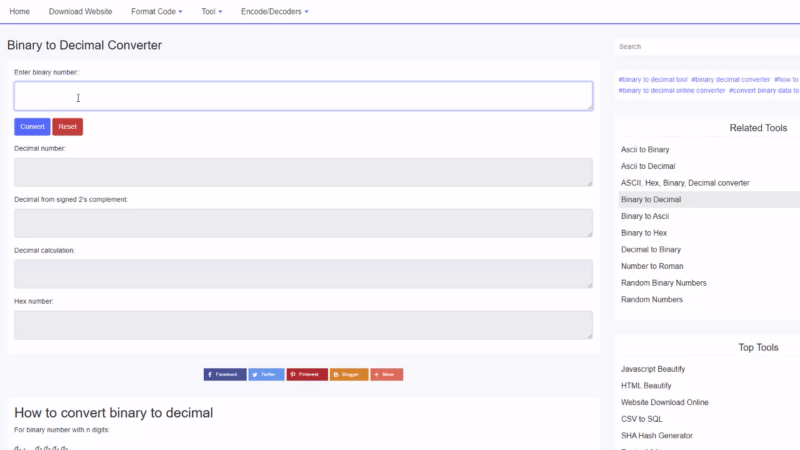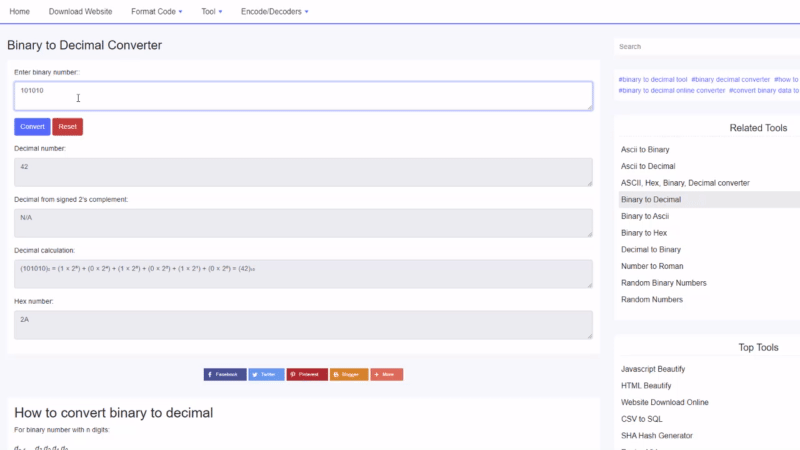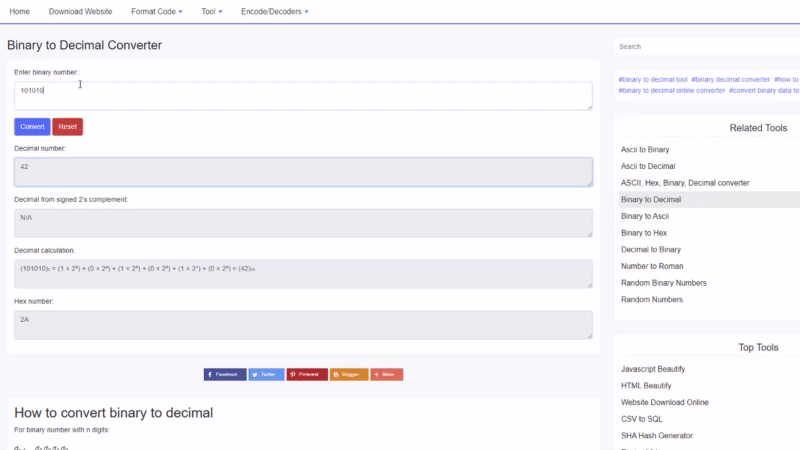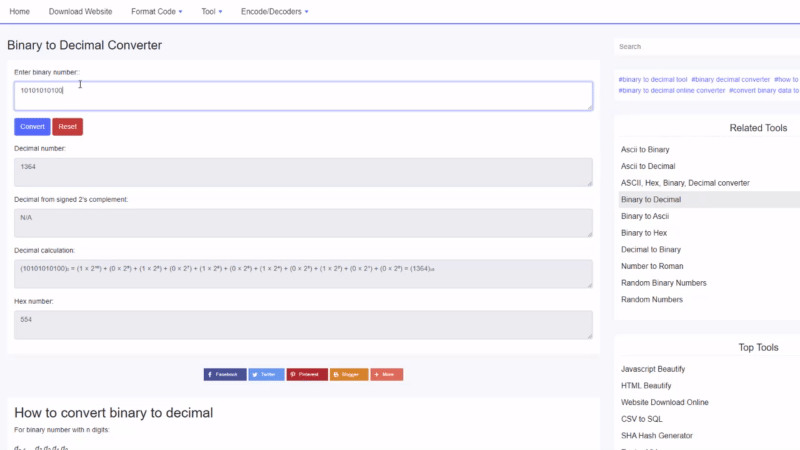
बाइनरीलाई दशमलवमा कसरी रूपान्तरण गर्ने
n अंक भएको बाइनरी नम्बरका लागि:
d n-1 ... d 3 d 2 d 1 d 0
दशमलव संख्या बाइनरी अंकहरूको योगफल (d n ) गुणा तिनीहरूको 2 (2 n ) को शक्ति बराबर हुन्छ :
दशमलव = d 0 × 2 0 + d 1 × 2 1 + d 2 × 2 2 + ...
बाइनरी देखि दशमलव उदाहरण
100010 2 को दशमलव मान पत्ता लगाउनुहोस् :
| बाइनरी नम्बर: | १ | ० | ० | ० | १ | ० |
|---|---|---|---|---|---|---|
| २ को शक्ति: | २ ५ | २ ४ | २ ३ | २ २ | २ १ | २ ० |
100010 2 = 1⋅2 5 +0⋅2 4 +0⋅2 3 +0⋅2 2 +1⋅2 1 +0⋅2 0 = 34 10
दशमलव प्रणाली
दशमलव अंक प्रणाली सबैभन्दा सामान्य रूपमा प्रयोग हुने र दैनिक जीवनमा मानक प्रणाली हो। यसले यसको आधार (रेडिक्स) को रूपमा नम्बर 10 प्रयोग गर्दछ। त्यसकारण, यसमा 10 प्रतीकहरू छन्: 0 देखि 9 सम्म संख्याहरू; अर्थात् ०, १, २, ३, ४, ५, ६, ७, ८ र ९।
बाइनरी प्रणाली
बाइनरी संख्या प्रणालीले यसको आधार (रेडिक्स) को रूपमा नम्बर 2 प्रयोग गर्दछ। आधार-२ अंकीय प्रणालीको रूपमा, यसले केवल दुई संख्याहरू समावेश गर्दछ: ० र १।
बाइनरी देखि दशमलव रूपान्तरण तालिका
| बाइनरी नम्बर | दशमलव संख्या | हेक्स नम्बर |
|---|---|---|
| ० | ० | ० |
| १ | १ | १ |
| १० | २ | २ |
| ११ | ३ | ३ |
| १०० | ४ | ४ |
| १०१ | ५ | ५ |
| ११० | ६ | ६ |
| १११ | ७ | ७ |
| १००० | ८ | ८ |
| 1001 | ९ | ९ |
| १०१० | १० | ए |
| 1011 | ११ | बि |
| ११०० | १२ | सी |
| ११०१ | १३ | D |
| १११० | १४ | इ |
| ११११ | १५ | एफ |
| 10000 | १६ | १० |
| 10001 | १७ | ११ |
| 10010 | १८ | १२ |
| 10011 | १९ | १३ |
| १०१०० | २० | १४ |
| १०१०१ | २१ | १५ |
| 10110 | २२ | १६ |
| 10111 | २३ | १७ |
| 11000 | २४ | १८ |
| ११००१ | २५ | १९ |
| ११०१० | २६ | १ ए |
| ११०११ | २७ | १ ख |
| १११०० | २८ | 1C |
| १११०१ | २९ | 1D |
| १११११० | ३० | १ ई |
| ११११११ | ३१ | १ एफ |
| 100000 | ३२ | २० |
| 1000000 | ६४ | ४० |
| 10000000 | १२८ | ८० |
| 100000000 | २५६ | १०० |