이진수를 십진수로 변환하는 방법
n자리의 이진수의 경우:
d n-1 ... d 3 d 2 d 1 d 0
십진수는 이진수(d n )에 2의 거듭제곱(2 n )을 곱한 값과 같습니다.
십진수 = d 0 ×2 0 + d 1 ×2 1 + d 2 ×2 2 + ...
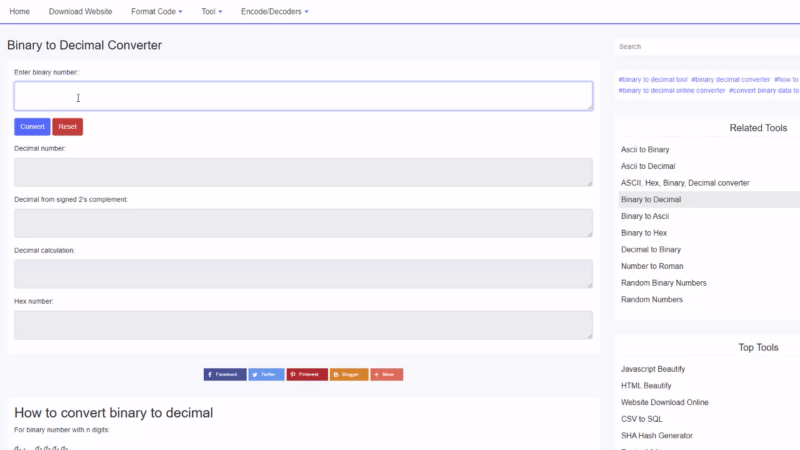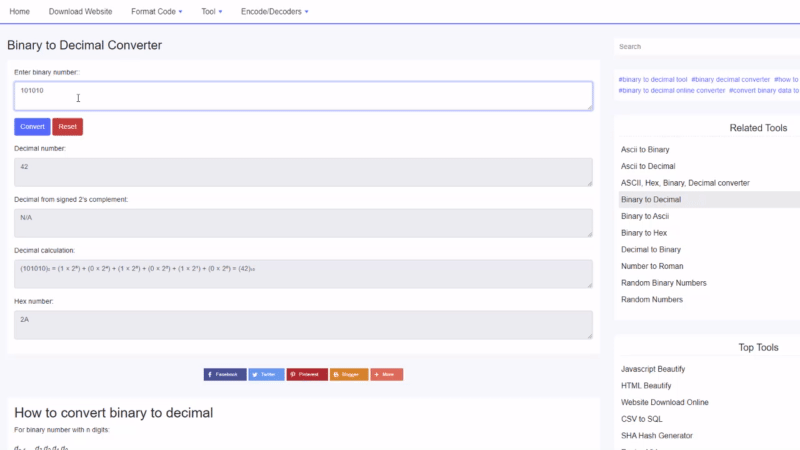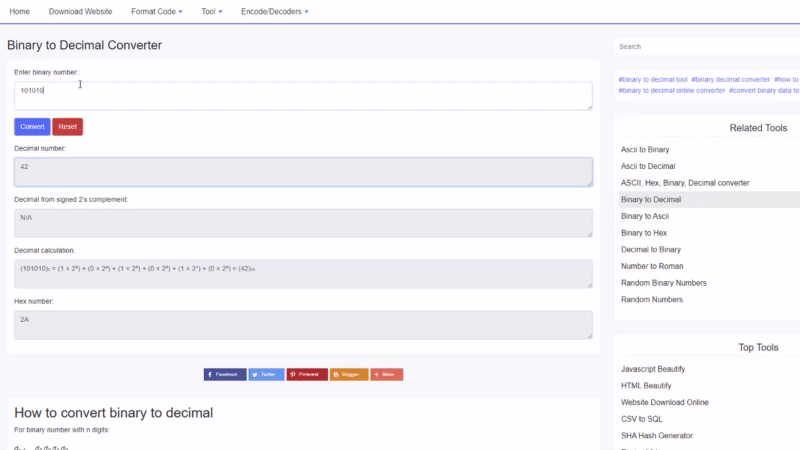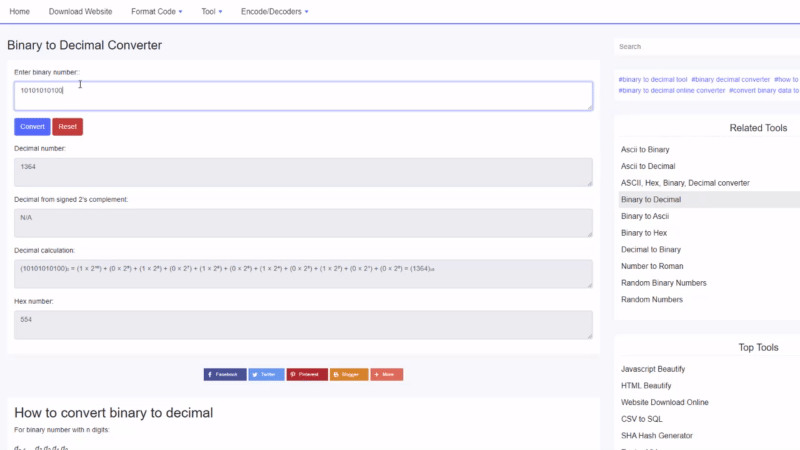
2진수에서 10진수로의 예
100010 2 의 10진수 값 찾기 :
| 이진수: | 1 | 0 | 0 | 0 | 1 | 0 |
|---|---|---|---|---|---|---|
| 2의 거듭제곱: | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
100010 2 = 1⋅2 5 +0⋅2 4 +0⋅2 3 +0⋅2 2 +1⋅2 1 +0⋅2 0 = 34 10
십진법
십진법 은 일상 생활에서 가장 일반적으로 사용되는 표준 체계입니다. 숫자 10을 기수(기수)로 사용합니다. 따라서 10개의 기호가 있습니다. 0에서 9까지의 숫자; 즉 0, 1, 2, 3, 4, 5, 6, 7, 8 및 9입니다.
바이너리 시스템
이진수 시스템 은 숫자 2를 기수(기수)로 사용합니다. 2진법 숫자 체계로 0과 1의 두 가지 숫자로만 구성됩니다.
2진에서 10진으로의 변환 테이블
| 이진수 | 10진수 | 16진수 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 삼 | 삼 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | NS |
| 1011 | 11 | NS |
| 1100 | 12 | 씨 |
| 1101 | 13 | NS |
| 1110 | 14 | 이자형 |
| 1111 | 15 | NS |
| 10000 | 16 | 10 |
| 10001 | 17 | 11 |
| 10010 | 18 | 12 |
| 10011 | 19 | 13 |
| 10100 | 20 | 14 |
| 10101 | 21 | 15 |
| 10110 | 22 | 16 |
| 10111 | 23 | 17 |
| 11000 | 24 | 18 |
| 11001 | 25 | 19 |
| 11010 | 26 | 1A |
| 11011 | 27 | 1B |
| 11100 | 28 | 1C |
| 11101 | 29 | 1D |
| 11110 | 30 | 1E |
| 11111 | 31 | 1F |
| 100000 | 32 | 20 |
| 1000000 | 64 | 40 |
| 10000000 | 128 | 80 |
| 100000000 | 256 | 100 |